

R-devel: betaBayes_1.0.zip, r-devel-UCRT: betaBayes_1.0.zip, r-release: betaBayes_1.0.zip, r-oldrel: betaBayes_1.0.zip Rcpp (≥ 0.11.1), splines, methods, coda, betareg See Zhou and Huang (2021, "Bayesian beta regression for bounded responses with unknown supports"). Model choice is carried out via the logarithm of the pseudo marginal likelihood (LPML), the deviance information criterion (DIC), and the Watanabe-Akaike information criterion (WAIC). When the response support is known to be (0,1), the above class of models reduce to traditional (0,1) supported beta regression models. The response variable is modeled using a four-parameter beta distribution with the mean or mode parameter depending linearly on covariates through a link function. The functions are prefixed with a-d for density-r for random number generation-p for cumulative distribution-q for quantile function. *Journal of the American Statistical Association*, *109*(505), 346–358.Provides a class of Bayesian beta regression models for the analysis of continuous data with support restricted to an unknown finite support. Probability distribution functions usually have four functions associated with them. For this distribution, the constraints c>0 8c, y c2(0 1), and P C 1 y c 1 8chave to hold. Probit Transformation for Kernel Density Estimation on the Unit Interval. The Dirichlet distributionas the generalization of the beta distributionis dened in Equation 1, where care the shape parameters for each variable. Kernel-Type Density Estimation on the Unit Interval.
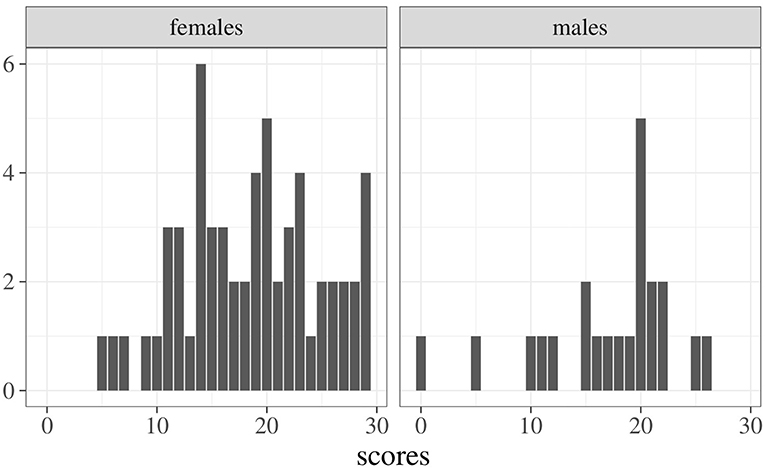
It uses the log-transform, but there are density estimators on using e.g. A consistent, unified and extensible framework for estimation of parameters for probability distributions, including parameter estimation procedures that allow for weighted samples the current set of distributions included are: the standard beta, The four-parameter beta, Burr, gamma, Gumbel, Johnson SB and SU, Laplace, logistic, normal, symmetric truncated normal, truncated normal, symmetric. all values from 0 to 1, but not 0 and 1 themselves, are permitted. I don't think the beta kernels perform that much better, if at all, than the "gcopula" kernels, which have their own benefits (being bona fide densities is one of them.)įinally, packages such as are specifically designed for speed. The beta distribution used in beta regression (Ferrari and Cribari-Neto 2004) is a model of data in the open (0, 1) interval. On the other hand, do you have yo use beta kernels? The "gcopula" (Jones, Henderson, 2007) kernel (in this package) is much faster, as we used its own, custom-made bandwidth selector. Chen (and others) probably made smarter bandwidth selectors, but we haven't implemented them. If this fails, send an email to following the. I think the problem is the bandwidth selection procedure, which defaults tocross-validation, which is the bottleneck. R is part of many Linux distributions, you should check with your Linux. Say 1000 individuals take a 100-item test where all items are equally difficult, and the true-score distribution is a four-parameter Beta distribution with location parameters l 0.25, u 0.75, alpha 5, and beta 3: set.seed(12) testdata <- rbinom(1000, 100, rBeta.4P(1000, 0.25, 0.75, 5, 3)) Since this test contains items which are all equally difficult, the true effective test.


 0 kommentar(er)
0 kommentar(er)
